공부 정리용 블로그입니다. 미숙한 실력으로 인해 표현이나 설명에서 많은 오류가 있을 수 있으니 참고 바랍니다 :)

NeRF보다 뛰어난 성능으로 유명하길래 한번 공부해보았다. Siggraph 논문인지라 mlp 적인 요소가 없는 특징이 있다고 한다.
Introduction
기존 NeRF는 countinuous scene representation이며, MLP 기반으로 최적화한다. 그러나 stochastic sampling으로 인해 많은 비용이 들고 노이즈를 발생시킨다는 문제가 있다. NeRF는 ray위의 임의의 점을 선택하여 해당 좌표를 학습한다. 만약 적절한 점을 선택하지 못한다면 (아무 의미 없는 점) 학습이 제대로 이루어지지 않게 된다.
본 논문은 3D Gaussian을 이용하여 visual quality와 빠른 시간 및 tile-based를 이용하여 real-time rendering을 가능하게 한다.
제시된 3가지 contributions로는,
- anisotropic 3D Guassian as representation
- optimization with adaptive density control
- fast, differential rendering
Methods
input으로는 정적 이미지와 SfM을 사용한 sparse point cloud가 주어진다. 각 point로부터 3D 가우시안 (덩어리라고 생각하면 된다.)을 생성하는데 position(mean), covariance matrix, opacity(alpha), color(SH coefficients)로 정의된다. 특히, color는 방향에 따라 성질이 바뀌며 spherical harmonics(SH) 기법을 이용한다.

** SH 내용 추가
본 모델의 효율성 핵심은 tile-based rasterizer이며, alpha-blending을 이용하여 동작한다.
Differential 3D Gaussian Splatting
먼저, SfM을 이용하여 normals 없는 sparse points로 시작한다. scene representation을 최적화하기 위해서, 미분 가능한 volumetric representation의 특징과 더불어 unstructed하고 explicit하여 빠른 렌더링을 가능하게 해야한다. 이를 위해 3D Gaussian을 선택하였다.
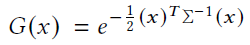
이는 blending process에서 alpha을 곱하면서 계산될 것이다.
추가로, 3D Gaussian을 2D로 렌더링하기 위해서는 다음 식을 이용한다.

여러 이유가 있어

R과 S를 따로 저장한다고 하니 아마도 covariance 값을 직접 구하는 것이 아닌 R, S를 이용해서 구하지 않을까 예상.
여기까지가 우리가 구해야하는 파라미터들을 알아보았다.
Optimization with adaptive denstiy control of 3D gaussian
본 모델의 핵심은 optimization이다. 이를 통해 정확한 dense set of 3D Gaussian을 만들 수 있다. view-dependant한 특징을 잘 나타내기 위해 color의 최적화가 중요하다.
Optimization
3D 가우시안의 covariance를 결정하는 파마리터는 representation의 compactness를 위해서 매우 중요하다. 넓은 동일한 공간을 적은 수의 커다란 3D 가우시안으로 대체하면서 효율적인 표현이 가능하기 때문이다.

Optimization은 rendering & comparing의 iteration으로 이루어지며, rendered image를 training dataset의 captured view와 비교하여 이를 기반으로 학습이 된다.
먼저 SfM point로부터 3D gaussian을 만들고, 초기 covariance matrix를 가까운 세 점으로부터 평균 거리 값으로 초기화한다.
Loss는 아래와 같이 정의하여, render image와 GT를 비교한다.

하지만 3D geometry의 2D projection의 모호함 때문에, geometry가 잘못 위치한 경우 이 geometry를 파괴하거나 움직일 수도 있어야 하는데, 이 부분이 Adaptive Control of Gaussians 이다.
Adaptive Control of Gaussians
초기 sparse set에서 더 잘 representation하는 denser set을 얻기 위해, 가우시안의 수와 unit volume 당 density를 조절한다. 100 iter 마다 densify하고 threshold보다 낮은 opacity를 가지는, 투명하다고 판단되는 가우시안을 삭제한다.
우리는 빈 공간을 채워야하기 때문에, geometric한 feature를 많이 놓친 (under-reconstruction) 부분에 집중하며, 또한 너무 많은 영역을 차지한 (over-reconstruction) 가우시안에도 집중한다. 러한 부분들은 아직 학습이 제대로 이루어지지 못한 곳으로 view-space positional gradient를 가지는 것을 확인하였다. gradient가 threshold보다 높으면 이를 densify해준다.

Under-Reconstruction일 경우, 해당 가우시안을 복사하여 positional gradient 방향으로 보낸다. 전체 볼륨을 증가시키고 가우시안의 수를 늘리는 것이다.
반면 Over-Reconstruction일 경우, 전체 볼륨은 유지하고 가우시안의 수를 늘린다. 따라서 처음의 큰 가우시안을 두 개로 나눈 다음, 원래의 가우시안 PDF에서 샘플링하여 초기 위치를 잡아준다.
optimize 과정에서 floater로 인해 가우시안의 수가 부정확하게 늘어날 수 있다. 이를 예방해주기 위해, 특정 주기마다 opacity를 0에 가깝게 세팅하여 필요한 부분은 이 값을 늘리고, 아닌 부분은 제거될 수 있도록 유도한다.
학습하다보면 가우시안들이 서로 엄청 중첩될 수도 있는데 위 방법을 이용하여 전체 가우시안 수를 잘 조절할 수 있다.

여기까지 학습하는 방법을 알아보았다. 이제는 이 3D를 2D 이미지로 변환(rasterization)하는 방법을 알아보자.
Fast Differential Rasterization for Gaussians

cull이라는 것은 렌더링 과정에서 특정 물체를 렌더링할지 말지 결정하는 과정이라고 해석하면 된다.
본 모델에서 사용하는 rasterization은 픽셀 단위가 아닌 타일 단위이다.
먼저, 이미지를 16 x 16로 나누면서 시작한다. 그리고 view frustum과 each tile에 대하여 비교한 후 Gaussians를 cull한다. 이때 Gaussian이 view frustum에 99% confidence로 교차하는 경우에 유지한다. 아마 view frustum 안에 있는 가우시안만 남겨둔다는 의미로 보인다. 각 타일에 대해서 비교하는 것은 해당 타일로 splat되는 가우시안만 다룬다는 의미로 해석하였다. 해당 타일로 splat되지 않으면 신경쓰지 않겠다는 것이다.
추가로, guard band를 이용하는데 near plane이나 far plane에 가까운 곳에 있는 가우시안도 2D covariance가 불안정하다는 이유로 제외한다.
각 가우시안에 key를 부여하는데 해당 가우시안의 공간적 깊이와 타일 ID를 결합한다. 이를 기반으로, sorting하고 blending 과정이 진행된다.