DDPM 간단 정리
논문을 음미하기 보다는 식 증명까지만 성공을 해서 간단하게 어떤 방식으로 진행되는지 살펴보겠다. code는 여유 있을 때 추가 예정
VAE처럼 식 하나하나를 코드로 생각하기보다는 해당 식의 의미에 집중하는 것이 좋아 보인다.
이 블로그에서 수식 증명을 정말 잘해놨음.

q(xt-1|xt)를 알고자 한다. 하지만 이것은 구할 수가 없어 해당 분포를 p_theta(xt-1|xt)로 근사화를 시켜서 해결한다. VAE와 같은 방식이다.
Objective funcion
잠시 VAE와 비교해보면,

VAE에서는 실제 분포와 가상의 분포를 근사화시킨다. 그러나 근사를 간접적으로 진행한다. p(x)를 상수로 보고, ELBO를 최대화함으로써 KL 값을 최소화하는 것이다. 나머지 식들도 다 ELBO를 이용해서 전개한다.
이처럼 어떠한 분포에 근사화시키기 위해서는 대상이 되는 분포를 알아야한다. 분포를 모르면서 근사화한다는 것은 말이 안됨. 그래서 우리는 대상 분포를 알아야 한다. q(xt-1|xt)는 모르지만, q(xt-1|xt, x0)은 알아낼 수가 있다. 정답값을 알면 할 수 있다는 것이다.
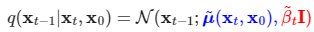


우리는 위의 분포에 맞출 것이다. 참고로, 알파와 알파_바, 베타는 모두 사전에 세팅해두는 상수 값이다. (베타를 학습해서 설정한다는 말도 있지만 본 논문에서는 사전 세팅한다.)

maximum likelihood 방식으로 진행한다. (ML에 대해서는 추가 공부 필요) KL은 무조건 0 이상이라서 위와 같이 식을 전개한다.

위와 같이 3개의 term으로 식을 구분할 수 있다.
L0는 상수이며, LT도 상수이다. XT는 가우시안 노이즈이므로, p_theta(XT)가 상수가 되기 때문이다.

우리가 설정한 p_theta는 이와 같은 함수가 될 것이고, 이 분포와 사전에 구해둔 실제 분포 간의 KL divergence를 구하는 task로 바뀌었다. (KL도 공부해보자)
Loss function
먼저, p_theta의 시그마 값은 사전 정의해둔 q(xt-1|xt, x0)의 분산에 맞추겠다고 하니 평균만 고려하면 된다.

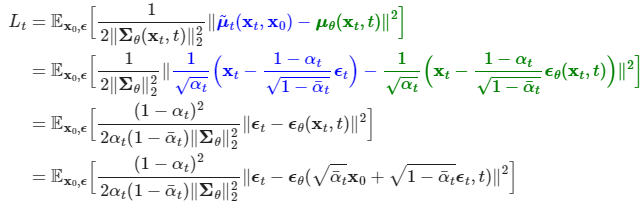
어느새, 평균을 비교하는 것이 아닌 노이즈를 구하는 task로 바뀐 것을 알 수 있다.

위와 같이 간단하게 바꾸었더니 실제로 성능이 더 좋았다고 한다.

위 알고리즘을 이용하여 간단하게 코드로 바꾼 깃헙을 보면 도움이 될거다.
마무리
이런 확률, 통계적인 논문을 읽을 때 주의할 점은 수식을 그대로 사용하지 않는다는 것이다.
objective function을 그대로 코드로 바꾸는 것이 아닌, 해석 (KLD)을 이용하여 간단한 loss function 만드는 것이다.
처음 블로그 보고 일단 수식부터 증명해봤는데, 그러다보니 생각보다 간단하게 전체적인 방법이 보였다. 여러 디퓨전 공부하다가 여유 생기면 원본 논문을 음미해봐야겠다.
+ Code
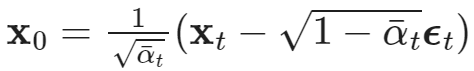
위 식과 q(xt-1|xt, x0) 식이 핵심이다.
def train(model, x_0): # 노이즈를 예측하는 U-Net 학습 목표
t = torch.randint(T, size=(x_0.shape[0], ), device=x_0.device)
eps = torch.randn_like(x_0)
# 앞에서 세팅해둔 eps로 x_t 만듦.
# 해당 x_t는 정답? 그 자체이다.
x_t = gather_and_expand(sqrt_alphas_bar, t, x_0.shape) * x_0 + \
gather_and_expand(sqrt_one_minus_alphas_bar, t, x_0.shape) * eps
# 이렇게 올바른 x_t를 가지고 eps을 예측 및 학습
loss = F.mse_loss(model(x_t, t), eps)
return loss
# 훈련을 할 때는 x0 주어짐.
# 랜덤 시점 t로 diffusing 후, x_t의 eps을 예측하는 것.
# 각 스텝에서의 eps을 모두 예측하는 것이 아닌 랜덤하게 샘플링한 스텝만 다룸.
# 여러 번 반복하면 각 스텝에 대한 eps가 가능할 것이라는 가정을 가지는 것이 아닐까 싶음.
# 최종적으로는 eps_t를 예측하는 것.def sample(model, x_T):
x_t = x_T
for time_step in reversed(range(T)):
t = torch.full((x_T.shape[0], ), time_step, dtype=torch.long, device=device)
eps = model(x_t, t)
x0_predicted = gather_and_expand(reciprocal_alphas_sqrt, t, eps.shape) * x_t - \
gather_and_expand(reciprocal_alphasm1_sqrt, t, eps.shape) * eps
'''
x0_predicted 그대로 결과로 아웃풋하지 않는 이유:
고정된 값. 상수로만 이루어져 있음.
이렇게 되면 똑같은 결과만 계속 뽑을거임.
불확실성을 모델링하는 것이 생성 모델의 핵심임. 계속 다르게 결과가 나와야한다는 뜻
그러기 위해서는 mean + variance 형태로 바꿔야함.
'''
mean = gather_and_expand(posterior_mean_coef1, t, eps.shape) * x0_predicted + \
gather_and_expand(posterior_mean_coef2, t, eps.shape) * x_t
z = torch.randn_like(x_t) if time_step else 0
var = torch.sqrt(gather_and_expand(sigmas, t, eps.shape)) * z
x_t = mean + var
x_0 = x_t
return x_0
# 샘플링은 x_T에서 시작함.
# 각 스텝에서 이전 스텝을 예측을 하는 것임.
# x0를 바로 구할 수 있음. 물론 이것도 틀린 것은 아니지만, diffusion은 불확실성을 모델링하는 것임.
# 그렇기 위해서 불확실성을 표현하는 평균 + 분산 형태로 바꿔줘야함.
def sample2(model, x_T):
x_t = x_T
for time_step in reversed(range(T)):
t = torch.full((x_T.shape[0], ), time_step, dtype=torch.long, device=device)
eps = model(x_t, t)
mean = gather_and_expand(reciprocal_alphas_sqrt_, t, eps.shape) * \
(x_t - gather_and_expand(eps_coeff, t, eps.shape) * eps)
z = torch.randn_like(x_t) if time_step else 0
var = torch.sqrt(gather_and_expand(sigmas, t, eps.shape)) * z
x_t = mean + var
x_0 = x_t
return x_0+ Improved DDPM
Improved-DDPM: Improved Denoising Diffusion Probabilistic Models
Alex Nichol, Prafulla Dhariwal (2021.02) [openAI] Abstract DDPM이 간단한 변경으로 높은 log-likelihoods 달성할 수 있다는 것을 보임 reverse diffusion 과정의 분산을 학습하면 더 적은 forward process로 큰 퀄리티 차이 없
dlaiml.tistory.com
위 블로그에서 설명 참고
새로운 모델을 제안하기보다는 성능 향상 방법 제안
결과물의 퀄리티와 log-likelihood는 무조건 비례하진 않는다. log-likelihood는 실제 분포를 얼마나 잘 학습했나, 잘 일반화했나를 나타낸다.
bits/dim: 한 픽셀당 더 적은 정보량을 가지고 있다. 정보 압축을 잘했다. 따라서 낮은 값일수록 더 높은 성능.
+ DDIM
추가강의 듣고 수정 예정
제대로 이해는 못했지만 전체적인 흐름은 DDPM가 별 차이가 없어보인다.
이해한 바로 써보겠다.
일단 DDIM 샘플링은 deterministic해서 input이 동일하면 output 또한 동일하다.

기존 DDPM에서는 forward를 markov로 정의를 했는데, 알고보니 이를 non-markov로도 식 변형이 된다는 것을 발견.

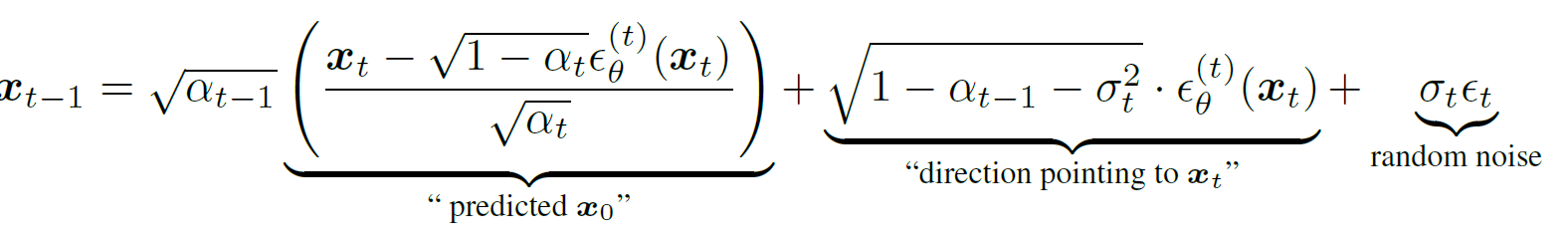
시그마 값만 0이면 DDIM이고 0이 아니면 DDPM과 동일하다. DDPM과 DDIM차이점은 시그마를 어떻게 설정하냐인 것 같다.

DDIM의 가장 큰 장점은 특정 스텝만 방문해서 값을 뽑아 DDPM보다 빠른 연산이 가능하다는 것이다. 만약 t 스템에서 t-2 스텝을 예측하고자 한다면, 알파와 노이즈 값을 그 스텝에 맞게 맞추면 된다.

DDIM이 deterministic하다고 해서 스텝에 따른 결과물이 완전히 동일하지는 않다. 스텝 간 결과물끼리는 서로 영향을 주기 때문이지 않을까 생각해서 바로 x0를 구하지는 않는 것으로 생각한다.
사실상 DDIM과 DDPM 차이는 별로 없어보이지만, xt-1에서의 "direction pointing to xt"이 중요해보인다. 시그마 값을 어떻게 설정하냐에 따라 DDIM이 될 수도, DDPM이 될 수도, different generative가 될 수 있다.
DDIM은 이런 generative를 일반화한 것이 아닌가 생각한다.
DDIM은 deterministic한 성격 때문에, latent 값이 x0에 대한 semantic 정보를 담고 있다. 그래서 latent 간의 semantic interpolation이 가능하다. (ex. 흑인 + 백인 => 황인)
DDPM은 불확실성을 가지고 있어서 latent가 무엇을 의미할지 몰라서 semantic interpolation이 불가능하다.
'Basis' 카테고리의 다른 글
| Transformers (study) (0) | 2024.09.08 |
|---|---|
| Generative Adversarial Nets (0) | 2024.09.01 |
| Autoencoders (0) | 2024.08.28 |
| Variational Auto-Encoder (0) | 2024.08.28 |
| [논문 review] Neural Discrete Representation Learning (VQ-VAE) (0) | 2024.07.18 |