GAN의 간단한 원리와 코드를 살펴보자.
Markov chains와 approximate inference를 사용하지 않는다는 것을 강조한다. 이러한 이유로 DDPM의 단점이 부각되기도 하였다.
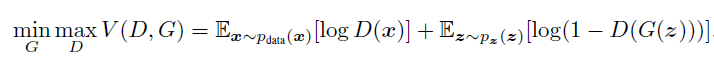
G를 학습하기 위해서는 위 식을 min하고, D를 학습시키기 위해서는 max한다고 생각하면 된다.
Pdata는 실제 train 데이터의 분포를, P(z)는 inference input로 가우시안 노이즈라고 이해하였다. 가우시안 노이즈를 입력으로 주고 G를 이용해서 output하면 특정 이미지가 되는 방식으로 진행된다.

파란색은 Pd, 검정색은 Pdata, 초록색은 Pg이다. D가 학습이 되면, G를 Pdata쪽으로 가이드하는 방식으로 학습이 진행된다.

이러한 이유로 식을 maximize하는 식으로 변경한다.

k step만큼 D를 학습시키고, 나머지 스텝에 G를 학습시키는 방식으로 진행한다. D를 먼저 최적화시키고 하면 D가 오버피팅이 되어 G의 학습에 방해를 줄 수 있어 이렇게 한다.
D를 학습할 때, ascending gradient라는 것을 확인할 수 있는데 이것은 D를 max 시키겠다고 생각하면 된다. 반대로 G는 min 방향으로 학습을 시키기 때문에, descending gradient이다.
Theorectical results
먼저, Pg = Pdata 일 때, global optimality를 만족시키는지 확인해야 한다. 분명 다른 논문을 읽을 때는 이렇게 증명을 하지는 않았는데 GAN의 경우에는 증명 과정에 있어 당황했다. 개인적으로 생각했을 때, 단순히 objective function을 만족한다고 되는 것이 아닌 Pg = Pdata라는 조건이 추가적으로 만족되어야해서 붙지 않았나 생각한다. (다른 논문들도 읽어보며 확인해봐야겠음.)
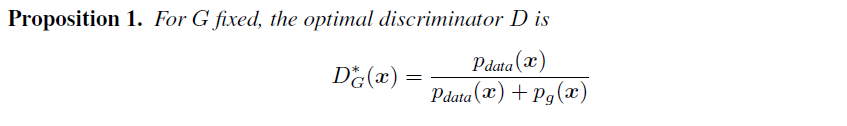
먼저 optimal D는 다음과 같이 나타낼 수 있으며, 이를 증명해보자.

** supp은 support라는 지지 집합으로 함수가 0이 아닌 값들을 갖는 점들의 집합이라고 한다. Pdata(x)가 0이 아닌 x의 집합이라고 해석한다. a, b가 {0, 0}이 아니라는 조건이 있어 이렇게 한 것으로 보인다.

D는 optimal D로 치면 식은 다음처럼 다시 쓸 수 있다. 이제는 optimal G를 구하는데 이때 Pg = Pdata를 증명하는 단계이다.

G를 학습시키기 위해서는 minimize를 해야하는데 JSD는 무조건 0 이상의 값으므로 최솟값은 -log4가 된다. 그리고 해당 최솟값은 Pdata = Pg일 때이므로, global optimality는 Pg = Pdata라는 것이 증명된다.
이번에는 알고리즘1에 따라 학습이 진행될 때, Pg가 Pdata로 잘 수렴될 수 있는지를 알아보자.
(해당 단락을 이해하지 못해 다른 블로그를 참고해서 추가 공부 필요함.) 결론은 적은 update만으로도 Pg는 잘 수렴할 것이다. D에 대해 여러 번 학습하고 나머지에 G를 학습하기에 나온 고민으로 보인다.
Code
이번 코드 역시 수식과는 괴리가 있다. 잘 적응이 안되는..
논문에서 수식적으로 증명하고 이를 코드로 표현한 것. (사실 코드 형태가 나오도록 증명 완료된 것)
class Generator(nn.Module): # noise로부터 이미지 생성자
def __init__(self):
super(Generator, self).__init__()
input_dim = opt.latent_dim + opt.n_classes + opt.code_dim
self.init_size = opt.img_size // 4 # Initial size before upsampling
self.l1 = nn.Sequential(nn.Linear(input_dim, 128 * self.init_size ** 2))
self.conv_blocks = nn.Sequential(
nn.BatchNorm2d(128),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 128, 3, stride=1, padding=1),
nn.BatchNorm2d(128, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 64, 3, stride=1, padding=1),
nn.BatchNorm2d(64, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
nn.Tanh(),
)
def forward(self, noise, labels, code):
gen_input = torch.cat((noise, labels, code), -1)
out = self.l1(gen_input)
out = out.view(out.shape[0], 128, self.init_size, self.init_size)
img = self.conv_blocks(out)
return imgclass Discriminator(nn.Module): # 생성자의 아웃풋 판별자
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(int(np.prod(img_shape)), 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid(),
)
def forward(self, img):
img_flat = img.view(img.size(0), -1)
validity = self.model(img_flat)
return validity # 진짜는 1, 가짜는 0for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Sample noise as generator input
# 가우시안 노이즈에서 샘플링
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
# Loss measures generator's ability to fool the discriminator
g_loss = adversarial_loss(discriminator(gen_imgs), valid)
g_loss.backward()
optimizer_G.step()
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = adversarial_loss(discriminator(real_imgs), valid)
# train 데이터 이미지를 True로 학습
# generator 학습 안하기 위해서 detach() 적용
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
# 생성자 이미지를 False로 학습
# 두 loss를 최소화하도록 학습
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
optimizer_D.step()
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
)
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
위 블로그에서는 실제 논문 상의 수식으로 코드를 구현하였다.
본 코드는 수식을 이해하고 해석해서 간단한 loss function으로 도출한 것이 아닌가하는 유추를 한다.
'Basis' 카테고리의 다른 글
| Training Neural Networks (study) (0) | 2024.11.18 |
|---|---|
| Transformers (study) (0) | 2024.09.08 |
| Diffusion (0) | 2024.08.30 |
| Autoencoders (0) | 2024.08.28 |
| Variational Auto-Encoder (0) | 2024.08.28 |