공부 정리용 블로그입니다. 미숙한 실력으로 인해 표현이나 설명에서 많은 오류가 있을 수 있으니 참고 바랍니다 :)
25/03/23 업데이트 되었습니다.
원래 계획은 원본 논문 Auto-Encoding Variational Bayes를 작성할 계획이었지만, 수학에 약해 실력을 쌓아서 다시 도전할 생각이다.
본 글에서는 참고1, 참고2를 이용하여 전체적인 VAE 진행 방향과 수식 증명을 다루고, code도 함께 살펴본다.
VAE는 latent z를 입력으로 하여, 그에 맞는 이미지를 출력하는 모델이다. 그래서 이 latent z를 샘플링하는 것이 중요하다.
임의로 z를 샘플링하고 이를 디코더에 넣어 이미지를 생성하는 방식으로 진행하면 데이터 표본에 있는 데이터조차 잘 생성하지 못한다고 한다. train set에 대해서도 잘 학습이 되지 않은 절망적인 상황이다.
그래서 VAE는 train set을 evidence로 줘서 p(z|x) 가우시안 분포를 사전 정의하고자 한다. 최소한 이것은 train set, 데이터 표본 x에 대해서는 잘 작동할 것이다.
이제 이상적인 확률 분포 p(z|x)를 구해야 한다. 그러나 우리는 이것을 구할 수 없다. p(z|x)를 p(z) x p(x|z) x 1/p(x)라고 표현할 수 있으며, p(x)를 구하는 것은 너무 복잡하다고 한다. (디테일하게 이해하면 수정 예정) 그래서 우리는 이 이상적인 확률 분포를 q(z|x)라고 근사화를 시키는데 이것은 variational inference라고 한다. 가우시안이라고 가정했을 때, 평균과 표준편차 값이 해당 네트워크의 output이다.

그럼 이제 생성 모델은 기존에 있던 g(x|z)와 이상적인 샘플링 함수 p(z|x)를 근사하는 Variable Inference 모델 q(z|x), 두 네트워크가 구성이 됩니다. 각 파이와 세타는 네트워크의 파라미터이다.
잠시 Maximum Likelihood (ML)를 알아보자.
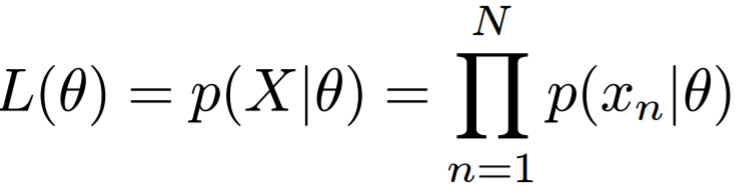
X라는 사건이 발생할 확률이며, 이는 각 datapoiint 확률의 곱으로 표현된다.

그리고 위 식은 곱으로 되어 있어 미분의 어려움이 있는데, 이를 로그로 변환하여 덧셈 형태로 표현하였다. 그리고 위 값을 최소화 시키는 것이 Maximum Likelihood이다. (L 값을 최대화 시킴)
다시 VAE로 돌아와서, VAE의 목적은 입력 데이터 x를 넣었을 때, 이 데이터를 가장 잘 생성하는 함수 p(x)의 ML을 구하는 것이다.

log(p(x))를 우리는 최대화하는 것이 목적이며, 위 식은 ELBO + KL으로 정의된다. 이때, ELBO라는 것은 KL이 무조건 0 이상이기에 log(p(x)) >= ELBO이므로 하한을 의미한다. 위 KL의 이상적인 분포와 approximation한 분포 간의 차이이다.
만약 logp(x) == ELBO로 만들 수 있다면, KL은 0에 가깝게 되어, 우리의 approximation이 True Posterior로 수렴한다.
ELBO 식을 다시 정리하면,
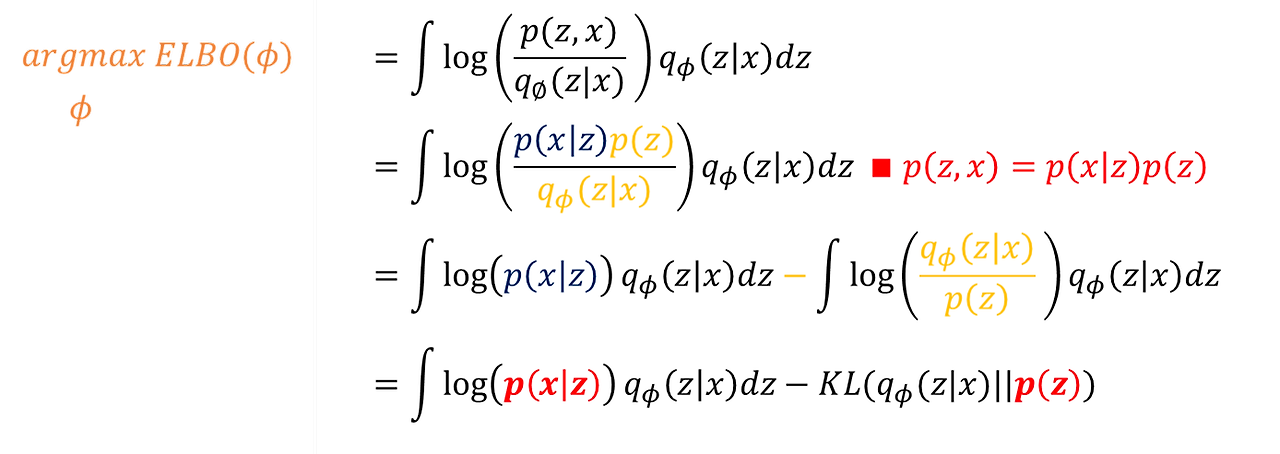
log(p(x))를 최대화시키고자 했던 우리의 목적은 이제 ELBO를 최대화시키는 것으로 바뀌었다. ELBO는 수식적으로 증명해봤을 때, log(p(x))를 넘을 수 없으므로 맘 편히 최대화하면 된다.
Loss function

오타 있지만 reconstruction error(- 부호까지 포함) 와 regularization error으로 나뉜다는 것을 확인하자.
reconstruction error는 x와 x'을 비교하는 것이며, regularization error는 각 x마다 서로 다른 가우시안을 가질텐데 이를 하나의 샘플링 함수(위에서는 표준 정규 분포)로 정규화시킨다.
Reparameterization trick
위 loss function에서 regularization term은 KL 공식을 이용해서 구하면 되지만, reconstruction term 은 학습 과정에서 구할 수 없다. (= 학습이 이루어지지 않는다.) 가우시안 분포에서 z를 랜덤하게 샘플링하는 것은 미분 불가능하기 때문에 encoder까지 gradient가 전달되지 않는다. 그래서 우리는 trick을 이용한다.
이전 방법은 평균과 분산을 구하고 이를 이용해서 분포를 그린 다음, 해당 분포에서 랜덤으로 뽑는 방식이다.
우리는 평균과 분산만을 이용해서 샘플링을 한다. 분포를 그리지 않고 뽑겠다는 것이다. 평균에 분산x노이즈 값을 더해서 마치 분포에서 샘플링한 흉내를 내는 것이다. 이 방식은 랜덤한 특징이 없기 때문에 gradient를 뒤로 전달할 수 있어 encoder까지 학습시킬 수 있다.
처음 보면 차이가 없어 보일 수 있지만 미분하고 이를 backpropagation하는 과정까지 생각해본다는 느낌을 알 수 있을 것이다.
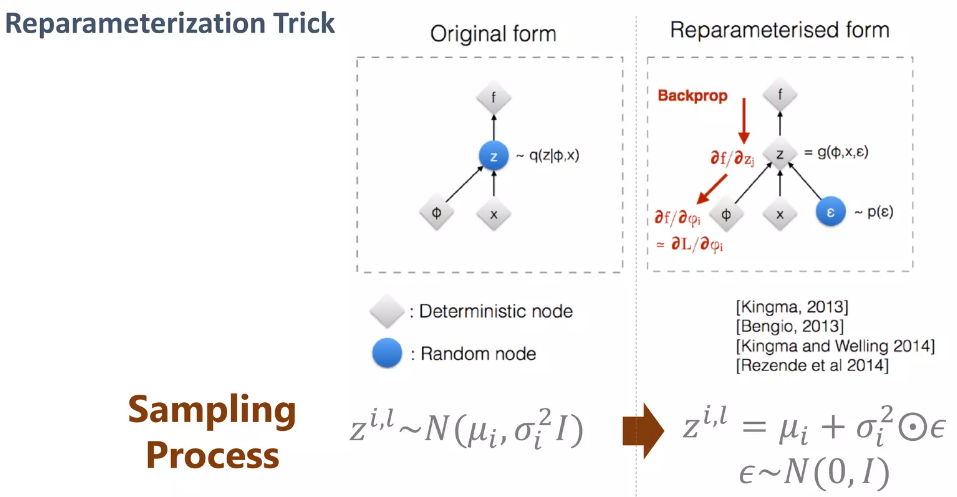


q의 분포를 위에서는 p(z) 표준 정규 분포 (평균:0, 표준편차: 1)로 설정하였다.
정리해보면, 이상적인 확률 분포와 최대한 유사한 분포를 생성하고 여기에서 샘플링을 하여 학습을 진행한다. 이때, 우리가가 만든 유사한 분포와 사전에 가정한 분포 간의 차이를 줄여주는 작업이 추가적으로 진행된다. 이때, 계산의 편의성을 위해 이를 표준 정규 분포로 가정하는 것이다.
Code
코드는 이론보다 훨씬 간단하다. 위의 기댓값, log 와 같은 식이 나오는데 우리의 코드에서는 쓰이지 않아 처음에 당황했다. 개인적으로는, 위의 복잡한 식들이 나온 이유는 해당 VAE 구조에 당위성을 부여한다고 생각한다. 왜 loss 가 이렇게 나오고 이렇게 하면 왜 잘되는지... 어떻게 보면, 식으로 구조를 도출하고 이를 코드화했다고 생각해도 되지 않을까 싶다.
class VanillaVAE(BaseVAE):
def __init__(self,
in_channels: int,
latent_dim: int,
hidden_dims: List = None,
**kwargs) -> None:
super(VanillaVAE, self).__init__()
self.latent_dim = latent_dim
modules = []
if hidden_dims is None:
hidden_dims = [32, 64, 128, 256, 512]
# Build Encoder
for h_dim in hidden_dims:
modules.append(
nn.Sequential(
nn.Conv2d(in_channels, out_channels=h_dim,
kernel_size= 3, stride= 2, padding = 1),
nn.BatchNorm2d(h_dim),
nn.LeakyReLU())
)
in_channels = h_dim
# input image size : 32 x 32 x 3
# 최종 image size : 2 x 2 x # of channels
# 그래서 곱하기 4 함. (2 x 2)
self.encoder = nn.Sequential(*modules)
self.fc_mu = nn.Linear(hidden_dims[-1]*4, latent_dim)
self.fc_var = nn.Linear(hidden_dims[-1]*4, latent_dim)
# Build Decoder
modules = []
self.decoder_input = nn.Linear(latent_dim, hidden_dims[-1] * 4)
hidden_dims.reverse() # 이렇게만 해도 list 역순됨.
for i in range(len(hidden_dims) - 1):
modules.append(
nn.Sequential(
nn.ConvTranspose2d(hidden_dims[i],
hidden_dims[i + 1],
kernel_size=3,
stride = 2,
padding=1,
output_padding=1),
nn.BatchNorm2d(hidden_dims[i + 1]),
nn.LeakyReLU())
)
# 채널은 2배씩 줄고, 사이즈는 2배씩 커짐.
# 여기까지 돌면 32 x 32 x 32
# 우리는 3 x 32 x 32 얻어야 함. (ConvTrnaspose로는 더이상 못함. 사이즈 커져버리니깐)
self.decoder = nn.Sequential(*modules)
self.final_layer = nn.Sequential(
nn.ConvTranspose2d(hidden_dims[-1],
hidden_dims[-1],
kernel_size=3,
stride=2,
padding=1,
output_padding=1),
# 32 x 64 x 64
nn.BatchNorm2d(hidden_dims[-1]),
nn.LeakyReLU(),
nn.Conv2d(hidden_dims[-1], out_channels= 3,
kernel_size= 3, padding= 1),
# 3 x 32 x 32
nn.Tanh()) def encode(self, input: Tensor) -> List[Tensor]:
# input: [B x C x H x W] (B: batch size)
result = self.encoder(input)
result = torch.flatten(result, start_dim=1)
# batch를 기준으로 뒷 부분은 하나의 값으로 곱해버리겠다.
mu = self.fc_mu(result)
log_var = self.fc_var(result)
return [mu, log_var] # 분포를 뽑아내는 것이 아니라 평균과 표준편차 출력
def decode(self, z: Tensor) -> Tensor:
"""
Maps the given latent codes
onto the image space.
:param z: (Tensor) [B x D]
:return: (Tensor) [B x C x H x W]
"""
result = self.decoder_input(z)
result = result.view(-1, 512, 2, 2)
result = self.decoder(result)
result = self.final_layer(result)
return result
# 생성된 이미지 출력 def reparameterize(self, mu: Tensor, logvar: Tensor) -> Tensor:
# 분산을 받아서 이를 루트 씌움.
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return eps * std + mu
def forward(self, input: Tensor, **kwargs) -> List[Tensor]:
mu, log_var = self.encode(input)
# 인코더에서 나온 값을 이용해서 z 샘플링 (trick 이용)
z = self.reparameterize(mu, log_var)
return [self.decode(z), input, mu, log_var] def loss_function(self,
*args,
**kwargs) -> dict:
"""
Computes the VAE loss function.
KL(N(\mu, \sigma), N(0, 1)) = \log \frac{1}{\sigma} + \frac{\sigma^2 + \mu^2}{2} - \frac{1}{2}
:param args:
:param kwargs:
:return:
"""
recons = args[0]
input = args[1]
mu = args[2]
log_var = args[3]
kld_weight = kwargs['M_N'] # Account for the minibatch samples from the dataset
# input과 output 이미지 픽셀 별 mse loss
recons_loss =F.mse_loss(recons, input)
# KLD 식 참고
# batch 별 평균 내리는 듯
kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim = 1), dim = 0)
loss = recons_loss + kld_weight * kld_loss
return {'loss': loss, 'Reconstruction_Loss':recons_loss.detach(), 'KLD':-kld_loss.detach()} def sample(self,
num_samples:int,
current_device: int, **kwargs) -> Tensor:
"""
Samples from the latent space and return the corresponding
image space map.
:param num_samples: (Int) Number of samples
:param current_device: (Int) Device to run the model
:return: (Tensor)
"""
# 훈련 데이터를 정규 분포로 보내고, 이를 표준 정규 분포로 보내는 방식으로 훈련 데이터를 표준 정규 분포로 바꿈.
# 표준 정규 분포로 근사화된 분포를 이용하여 디코더를 학습
# 학습된 디코더에 표준 정규 분포 샘플링을 넣어 진행한다.
# 디코더는 표준 정규 분포의 값을 이용해서 그럴 듯한 이미지를 뽑아내도록 학습이 되었을 것이다.
# 새로운 데이터를 생성하는 것.
z = torch.randn(num_samples,
self.latent_dim)
z = z.to(current_device)
samples = self.decode(z)
return samples
def generate(self, x: Tensor, **kwargs) -> Tensor:
"""
Given an input image x, returns the reconstructed image
:param x: (Tensor) [B x C x H x W]
:return: (Tensor) [B x C x H x W]
"""
# input data를 다시 recon하는 것.
# experiment.py에서 test input을 recon할 때 사용됨.
# recons = self.model.generate(test_input, labels = test_label)
return self.forward(x)[0]* 25/03/23 *
지금 생각하는 VAE는 다음과 같다.

우리는 위의 p(x) 값을 최대로 만들고자 한다. (maximum likelihood)
먼저 VAE는 모든 샘플 x는 어떠한 z 값에서부터 만들어졌다. 라는 가정을 가지고 시작한다.
첫번째 전략은, p(z|x)를 구하는 것이다. 이것이 의미하는 것은, 현재의 샘플 데이터가 어느 z에서 왔는지 이다. 인코더 q가 생성하는 z를 p(z|x)에 맞춰서 모델을 학습시킬 수 있다면, inference할 때에도 p(z|x)에서 샘플링한 값을 디코더에 넣어서 generation할 수 있다.
그러나 p(z|x)를 구할 수 없다. 그렇기 때문에 첫번째 term인 KL 항을 만족시키는 것은 포기하고, 두번째 term ELBO 항을 최대화하는 방향으로 학습하게 된다.

두번째 전략인 ELBO 최대화는 다음의 가정이 사용된다.
- prior (p(z)) 는 가우시안 분포를 가진다.
샘플링을 쉽게 하기 위해 p(z)는 가우시안 분포로 가정하고, encoding z 값의 분포를 p(z) (샘플링 공간)으로 맞추는 것은 KL 항이 도와준다. encoding 분포에서 샘플링된 z를 디코더에 넣어 x가 복원되는지 확인하는 과정이 전체 VAE 과정이다.
Q. 이때, 두번째 항에서 z를 가우시안 분포가 아닌 학습 중인 encoding 분포에서 샘플링하는 이유는 무엇일까?
A. 단순히 바로 가우시안 분포에서 z를 샘플링하게 되면, 두번째 term은 인코더를 학습시키지 못하게 된다. end-to-end로 학습되는 것이 아닌, 각 모듈별로 학습되는 느낌이랄까.
'Basis' 카테고리의 다른 글
| Transformers (study) (0) | 2024.09.08 |
|---|---|
| Generative Adversarial Nets (0) | 2024.09.01 |
| Diffusion (0) | 2024.08.30 |
| Autoencoders (0) | 2024.08.28 |
| [논문 review] Neural Discrete Representation Learning (VQ-VAE) (0) | 2024.07.18 |