공부 정리용 블로그입니다. 미숙한 실력으로 인해 표현이나 설명에서 많은 오류가 있을 수 있으니 참고 바랍니다 :)
autoencoder에 관해 찾아보던 중, autoencoders 서베이(?) 논문을 발견하였다. 요즘 사용되는 다양한 종류의 오토인코더와 이것들의 다양한 사용법을 다룬 논문이라 가볍게 읽어보았다.
Autoencoders
오토인코더는 이것의 인풋을 재구현하기 위해 훈련되었다. 그래서 이것의 메인 목표는 데이터의 'informative' representation을 비지도학습하는 것이다.

위 식을 최소화시키는 A(encoder), B(decoder)를 찾는 것이 목적이다. 식을 이렇게 표현한 것을 처음 봐서 넣어봤다.
데이터를 압축한다는 관점에서 봤을 때, 오토인코더를 PCA의 일반화라고 생각할 수도 있다. linear뿐만 아니라 non-linear까지 표현할 수 있다.
Regularized autoencoders
학습을 하다보면 identity operator를 가질 수 있게 때문에 regularization이 필요하다. 가장 흔한 방법은 input보다 차원이 작은 representation을 만드는 것이고 이를 bottleneck이라고 부른다. 1차원으로 압축을 하더라도 인코더와 디코더의 capacity가 충분히 크면 오버피팅이 가능하기도 하다.
만약 인풋보다 더 큰 차원으로 압축된다면 인코더가 identity function이 될 위험이 존재한다. bottleneck, 즉 저차원으로 압축하는 것 외에도 다른 방법들이 존재하는데, 우리는 hereafter라고 부른다. 인풋과는 다른 값을 가지도록 하는 것을 말한다.
오토인코더에는 bias-variance tradeoff라는 것이 존재한다. 인풋을 그대로 잘 구현하기를 원하면서 동시에 저차원의 일반화를 잘하는 representation을 동시에 원한다. 이러한 tradeoff를 다룰 필요가 있다.
Sparse Autoencoders
hidden activations에 sparse를 부여해서 tradeoff를 다룬다. 2가지의 sparsity regularization을 소개한다. (여기에서 말하는 sparse가 무엇인지는 잘 모르겠으나, 특정 노드의 가중치에 쏠려 오버피팅되는 것을 막겠다는 의미로 보인다.)
1. L1 regularization 적용

여기에서 a는 i번째 히든 레이어의 노드이다.
2. KL divergence 적용

각 노드들이 0과 1 값을 가지는 베르누이 (Bernouli) 분포를 따르며, 목표 확률 p와 empirical p'를 비교한다.
p'은 활성화된 노드 수/ 전체로 구해진다. p'을 조절하며 서로의 값을 맞춘다.

Denoising Autoencoders
해당 오토인코더는 regularization으로 보일 수도 있지만, robust한 오토인코더 (for error correction)로도 보일 수도 있다.

원본 인풋에 노이즈를 추가하여 corruptional input을 만들고, 해당 인풋으로 나온 x'과 원본 인풋 간의 비교를 통해 모델을 학습한다. 노이즈한 이미지로부터 깨끗한 이미지를 만들도록 학습 받기 때문에 error correction이라고 생각한다.
Contractive Autoencoders
denoising 오토인코더와를 조금 결이 다르게, 입력 데이터에 작은 perturbation이 있어도, latent representation을 덜 민감하게 만들어 일반화된 특성을 가지게 한다.

위 두개의 term은 서로 다른 방향으로 작동하는데, Jacobian norm을 최소화하면, latent representation의 값이 서로 유사해져 reconstruction을 어렵게 만든다. 메인 아이디어는 중요하지 않은 latent representation의 variation을 자코비안 regularization term을 이용하여 사라지게 하고, 중요한 variation은 reconstruction error를 통해 유지되게 한다.
Variational Autoencoders
Applications of autoencoders
Autoencoders as a generative model
posterior q(z|x)는 prior p(z)로 정규화되었고, 한번 학습되면 같은 prior에서 샘플링을 통해 디코더에 넣을 수 있다. 디코더는 p(x|z)로부터 x를 생성하도록 훈련되어 그럴듯한 새로운 데이터를 생성할 수 있다.

Use of autoencoders for classification
오토인코더는 비지도학습으로 되어 있지만, 반지도 학습에서도 분류 성능을 높이고자 사용될 수 있다. 라벨이 없는 데이터로 오토인코더를 학습하고 오토인코더의 인코더를 분류 모델과 연결하여 라벨이 있는 데이터에 대해 훈련한다.
이것의 중요한 가정은 같은 라벨의 데이터는 유사한 latent 표현을 가져야한다는 것이다. 비지도학습된 오토인코더에서 디코더는 떨어지고 인코더는 네트워크의 첫번째 파트가 된다. 인코더는 그대로 사용될 수도 있고 파인튜닝될 수도 있다.
오토인코더는 분류 모델에 대해 regularization technique으로 사용될 수도 있다.

classification head에 더불어, reconstruction head가 달려있어 분류 모델의 과적합을 방지할 수 있다.
Use of autoencoders for clustering
많은 클러스터링 알고리즘은 데이터의 차원에 민감하고, 차원의 저주를 받는다. 차원의 저주는 데이터의 차원이 증가할수록 데이터 분석 및 학습 알고지름이 직면하는 문제가 증가하는 현상이다. 고차원 데이터에서는 데이터 포인트들이 희소해지고, 데이터 간의 거리나 밀도에 대한 의미가 왜곡된다고 한다. (GPT 왈)
클러스터링에서의 단점은 vanilla 오토인코더의 임베딩 값은 reconstruction을 위해서지, clustering을 위해서 학습되지 않았다는 것이다. 하나의 대안은 임베딩 값 또한 학습을 하는 것인데, 기존 loss function에 임베딩과 클러스터 중심 간의 거리를 penalize하는 것을 추가한다.
Use of autoencoders for anomaly detection
anomaly detection이란 이상 탐지이다. 정상 데이터로부터 정상 profile을 학습하고, 정상 profile에 부합하지 않는 샘플을 anomalies로 분류한다. 정상 데이터에 대해서는 낮은 reconstruction error를 보이고, 이상 데이터에 대해서는 높은 값을 보인다.
Use of autoencoders for recommendation systems
추천 시스템은 사용자의 선호도나 물건에 대한 친화력을 예측한다.
추천 시스템에서 많이 쓰이는 방법으로 Collaborative Filtering (CF)가 있다. 이것은 다른 유저의 선호도를 이용하여 해당 유저의 선호도를 추론한다. 인간의 선호도는 서로 강한 상관관계가 있다는 가정 하에 진행된다.
추천 시스템에서 가장 베이직한 오토인코더 사용의 예시는 AutoRec 모델이다. user-based AutoRec (U-AutoRec)과 item-based AutoRec (I-AutoRec)이 있다.
M을 유저, N을 아이템 수라고 할 때, rm은 유저m의 각 N개 아이템에 대한 선호도 벡터이다.

우리는 prediction time 때, reconstruction vector를 구해 해당 유저가 선호하는 아이템을 찾는다.
반대로 I-AutoRec 같은 경우에는,
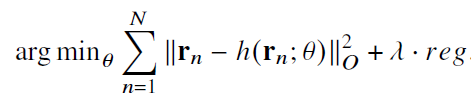
각 아이템에 대한 preference vector를 구해 높은 선호도를 가진 잠재 유저를 찾는다.
Use of autoencoders for dimensionality reduction
텍스트나 이미지 같은 real world 데이터는 sparse 고차원으로 표현된다. 많은 모델들이 고차원 공간에서 동작하지만, 이는 curse of dimensionality를 유발할 수 있다. 차원 축소의 목적은 "intrinsic dimensionality"라고 불리는 lower dimensionality manifold를 학습하는 것이다.
클래식한 예시로는 Principle Component Analysis (PCA)가 있다. 이것은 데이터를 저차원 공간으로 linear projection하는 것이다. linear projection에서는 가장 좋은 방법이지만, 오토인코더와 같은 non-linear 방법은 더 좋은 성능을 가진다.
Linear Discriminant Analysis (LDA)는 linear subspace를 찾는 것으로, 서로 다른 클래스를 잘 구별한다.
추가로, ISOMAP은 저차원 manifold를 학습한다.
Advanced autoencoder techniques
이미지에 대한 오토인코더의 reconstruction quality를 보면, 결과 이미지가 흐리다는 단점이 있다. 이것은 사용된 loss에 이유가 있는데, 결과물이 얼마나 realistic한지 고려를 안하고, 인풋 이미지는 흐리지 않다는 prior knowledge를 사용하지 않기 때문이다. 이것을 해결하는 방법들이 나오고 있다.
Autoencoders and generative adversarial networks
Generative Adversarial Networks (GANs)는 생성자와 구별자로 이루어져있다. 이들은 생성된 데이터의 퀄리티를 높이면서 학습이 진행되어 생성된 이미지가 보다 realistic하지만 컨트롤에 cost가 높다. VAE loss function에서의 KL divergence를 GAN의 discriminator 모델로 바꾸는 등, 많은 변형과 결합이 있다.
Adversarially learned inference (ALI)
GANs는 mode collapse라는 단점을 가지고 있는데, 이것은 생성된 데이터가 전체 데이터 분포의 일부만 반영하고 나머지는 놓치는 현상을 말한다. ALI는 VAEs와 GANs를 결합하여 해결한다.
VAE의 인풋과 아웃풋 사이의 loss function 대신, (input sample, z ~q(z|x))와 (decoder output, z ~p(z)) 사이에 discriminator가 사용된다. 구별자를 속이기 위해 디코더는 realistic 결과를 뽑게 된다.
Deep feature consistent variational autoencoder
원본 이미지와 reconstructed 이미지가 주어졌을 때, 이들의 픽셀 간 차이를 계산하는 것 대신 픽셀 간의 상관관계를 고려하는 방법이 있다. 모델 내에서 두 이미지의 representation을 비교하는 것이다. 다양한 레이어에서 이미지 간의 차이를 계산함으로써 더 realistic한 차이를 측정할 수 있다.
(GAN, Wasserstein-GAN, PixelCNN은 논문을 직접 읽어볼 예정이다.)
Conclusions
오토인코더는 잘 압축되고 의미있는 representation을 얻는 것이다. 우리는 유의미한 representation을 얻고자 하며, 동시에 reconstruction에 좋은 representation을 얻으려고 한다. 이러한 trade off 상황에서 모든 니즈를 충족할 수 있는 아키텍처를 찾는 것이 중요하다.
'Basis' 카테고리의 다른 글
| Transformers (study) (0) | 2024.09.08 |
|---|---|
| Generative Adversarial Nets (0) | 2024.09.01 |
| Diffusion (0) | 2024.08.30 |
| Variational Auto-Encoder (0) | 2024.08.28 |
| [논문 review] Neural Discrete Representation Learning (VQ-VAE) (0) | 2024.07.18 |